Cómo calcular el par de las bisagras: Guía paso a paso

El par de las bisagras es un parámetro crítico en el diseño de cubiertas giratorias, paneles de puertas o pantallas. Determina el efecto de amortiguación y el equilibrio cuando los componentes se abren y se cierran. Un diseño incorrecto del par de torsión puede hacer que los paneles caigan sin control, dificultar la apertura o provocar incidentes de seguridad. Comprender el cálculo del par es esencial para mejorar la seguridad del producto y la experiencia del usuario.

Este artículo comienza con la definición física del par, analiza sistemáticamente los factores que influyen y las fórmulas de cálculo, y demuestra el proceso mediante ejemplos prácticos. Este artículo abarca la definición de par, las variables clave, ejemplos de cálculo, factores de seguridad y métodos de verificación, lo que permite a los diseñadores comprender rápidamente los principios esenciales.

Funciones básicas del par de bisagra

Apoyo y amortiguación

Las bisagras soportan el peso del panel y ofrecen resistencia durante la apertura, garantizando la estabilidad en cualquier ángulo.

Equilibrio y seguridad

Un par de apriete adecuado permite que un panel se abra de forma equilibrada, evitando que caiga repentinamente por su propio peso. Un par de apriete insuficiente crea riesgo de caída, mientras que un par de apriete excesivo dificulta la apertura y puede provocar concentración de tensiones.

Mayor operatividad

Las bisagras de torsión (o "bisagras de fricción") permiten la colocación libre en cualquier ángulo sin mecanismos de apoyo adicionales.

Objetivo

Este artículo muestra progresivamente la definición, la fórmula de cálculo y el proceso de diseño del par de las bisagras. Incluye: definición de la fórmula de cálculo, ejemplos paso a paso, introducción de ajustes del factor de seguridad y métodos de verificación detallados. Por último, ofrece referencias de selección de par para diversos escenarios de aplicación, capacitando a los ingenieros para dominar el diseño de par de bisagra.

Comprender los fundamentos: ¿Qué es el par de bisagra?

Definición y cálculo del par de bisagra

Definición física

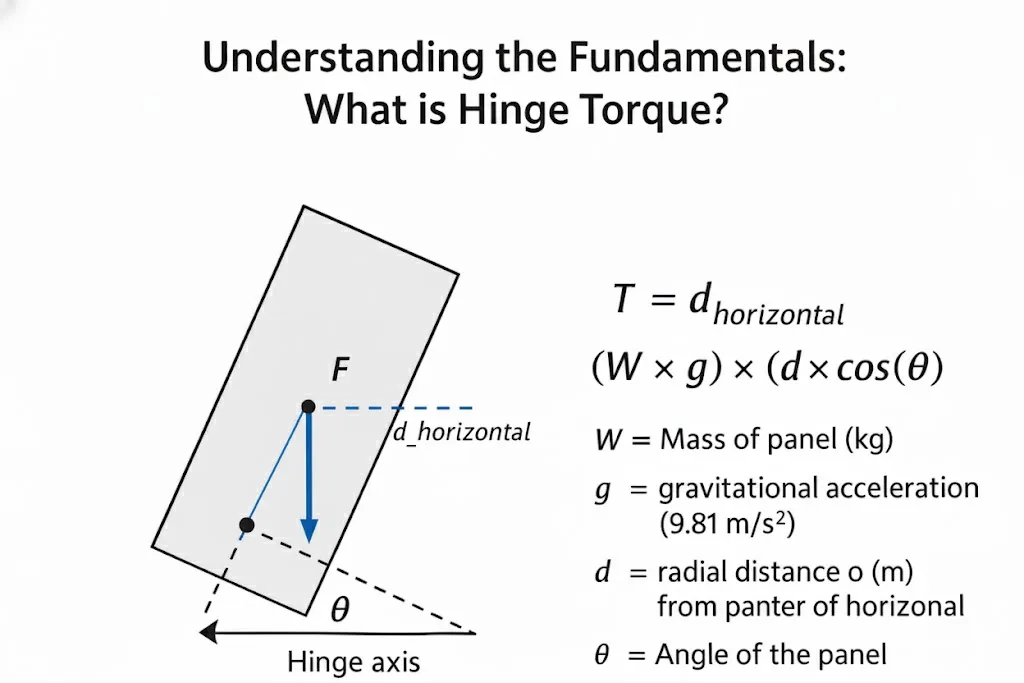
El par ($T$) es la fuerza de rotación, definida como la fuerza aplicada ($F$) multiplicada por la longitud del brazo de palanca ($d$). Para una bisagra, la fuerza primaria es el peso del panel (masa $\times$ aceleración gravitatoria) actuando en su centro de gravedad. El par se suele medir en N-m (Newton-metros).

La fórmula fundamental se expresa como:
$T = F \times d_{\text{horizontal}} = (W \times g) \times (d \times \cos(\theta))$

Dónde:

• $W$ = Masa del panel (kg)
• $g$ = Aceleración gravitatoria (≈9,81 m/s²)
• $d$ = La distancia radial (distancia en línea recta) desde el centro de gravedad del panel hasta el eje de la bisagra (m)
• $d_{text{horizontal}}$ = El brazo de palanca horizontal (m), que es el componente de $d$ que realmente produce el par. Se calcula como $d_{text{horizontal}} = d \times \cos(\theta)$
• $\theta$ = El ángulo del panel con respecto al plano horizontal.
• La fórmula fundamental se expresa como:

T=F×dhorizontal=(W×g)×(d×cos(θ))T = F \times d_{\text{horizontal}} = (W \times g) \times (d \times \cos(\theta))T=F×dhorizontal=(W×g)×(d×cos(θ))

Esta fórmula muestra correctamente que el par es MÁXIMO ($T = Wgd$) cuando el panel está horizontal ($\theta = 0°$), ya que el brazo de palanca es el más largo. El par es CERO cuando el panel está vertical ($\theta = 90°$), porque la línea de acción del peso del panel pasa por el eje de la bisagra y el brazo de palanca es efectivamente cero.

Par estático frente a par dinámico

• Par estático: La fuerza de rotación necesaria para mantener el panel inmóvil en un ángulo determinado (venciendo a la gravedad). Este es el objetivo principal de nuestro cálculo.
• Par dinámico: El par adicional necesario para vencer la inercia (para iniciar o detener el movimiento) y las fuerzas de amortiguación.

Normalmente, el diseño se centra primero en calcular el par estático máximo y, a continuación, tiene en cuenta los efectos dinámicos en función de la aplicación.

Papel funcional en el diseño

El par de torsión de las bisagras controla el equilibrio del panel, permite el posicionamiento libre y evita el cierre repentino. Por ejemplo, las bisagras de torsión utilizan mecanismos de fricción internos para mantener inmóviles las cubiertas. Un par de torsión adecuado garantiza un funcionamiento estable y suave.

Factores clave que afectan al par de las bisagras

Peso de la cubierta (W): El par es directamente proporcional al peso del panel.

Centro de gravedad (d): Cuanto mayor sea la distancia horizontal (brazo de palanca) entre el centro de gravedad del panel y el eje de la bisagra, mayor será el par necesario. Para paneles asimétricos, debe determinarse el centro de gravedad real.

Número de bisagras (N): Varias bisagras comparten la carga de par total. Para una disposición simétrica, lo ideal es que el par total se distribuya uniformemente: $T_{\text{por_bisagra}} = T_{\text{max}} / N$ (Supone una distribución simétrica de la carga). / N$ (Supone una distribución simétrica de la carga. Para paneles asimétricos en los que el centro de gravedad no está centrado entre las bisagras, el par total ($T_{text{max}}$) sigue siendo el objetivo. Sin embargo, los diseñadores deben asegurarse de que el panel sea lo suficientemente rígido para evitar el pandeo o la torsión durante el funcionamiento).

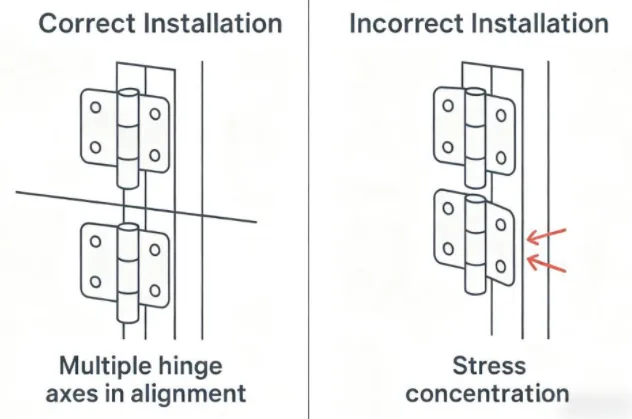
Ángulo de instalación y rango de rotación ($\theta$): El par es máximo cuando el panel está horizontal ($\theta = 0°$) y mínimo (cero) cuando está vertical ($\theta = 90°$). Los cálculos de diseño deben utilizar siempre como base el escenario de par máximo (la posición horizontal).

Amortiguación y fricción: La fricción interna en las bisagras de torsión proporciona la fuerza de "sujeción". Factores ambientales como la temperatura, el polvo o las condiciones de lubricación pueden afectar al par real. Las altas temperaturas pueden reducir la viscosidad de la grasa amortiguadora (disminuyendo el par), mientras que las bajas temperaturas o la contaminación pueden aumentar la fricción(Laesecke y otros, 2019, NIST).

Cálculo de fórmulas y análisis de pasos

Fórmula básica

El cálculo del par fundamental de la bisagra es:
$T = W \times g \times d \times \cos(\theta)$

A efectos de diseño, debemos encontrar el par máximo ($T_{text{max}}$), que se produce cuando el panel está horizontal ($\theta = 0°$, lo que significa $\cos(0°) = 1$).

La fórmula se simplifica a:
$T_{\text{max}} = W \times g \times d$

La fórmula de referencia de selección de un proveedor de bisagras, como "Par $T = L/2 \times m \times 9,8$ (en N-m)", se basa en este principio exacto. Supone:

• $m$ = masa ($W$)
• $L/2$ = distancia del centro de gravedad ($d$), suponiendo un panel uniforme en el que el C.G. está a la mitad de su longitud/anchura.

Ejemplo: Para un panel con $L=0,3$ m (por tanto $d=0,15$ m) y $m=2$ kg, el par máximo es:
$T_{text{max} = 0,15 \text{ m} \por 2 kg \por 9,81 \text{ m/s}^2 \aprox 2,94$ N-m.

Pasos del cálculo

Paso uno: Calcular el par máximo total ($T_{\text{max}}$)

Utilice siempre la fórmula de la posición horizontal ($T_{texto{máx}} = Wgd$) para hallar la carga más desfavorable.

Ejemplo: Un panel tiene una masa ($W$) de 8 kg, y su centro de gravedad ($d$) está a 0,25 m del eje de articulación.
$T_{\text{max}} = W \times g \times d$
$T_{text{max}} = 8 \text{ kg} \por 9,81 \text{ m/s}^2 \text{ m} por 0,25 \text{ m} \$ 19,62 N-m

Estos 19,62 N-m son el par estático total que debe poder soportar el sistema de bisagras para mantener el panel en su posición más pesada (horizontal).

Segundo paso: Distribución del par de las bisagras

Pasos de cálculo: Distribución del par de la bisagra (carga simétrica)

Si utiliza varias bisagras, divida el par máximo total por el número de bisagras ($N$).

En el ejemplo anterior, si se utilizan bisagras $N=2$:
$T_{texto{por_bisagra}} = T_{texto{máx}} / N = 19,62 / 2 \aprox$ 9,81 N-m por bisagra.

A continuación, seleccione dos bisagras con una capacidad mínima de 9,81 N-m, tras aplicar los factores de seguridad.

Factores de corrección y seguridad

• Factor de seguridad: Factor de seguridad: Multiplicar $T_{\text{max}}$ por 1.2-1.5 para tener en cuenta los errores de montaje, el envejecimiento de los materiales y las tolerancias de fabricación. Para movimientos rápidos o entornos de alta vibración, añada un margen adicional de 10-30%. En temperaturas extremas, consulte los datos del fabricante para la variación del par debido a los cambios de viscosidad de la grasa amortiguadora.
• Corrección dinámica de la carga: Para una apertura/cierre rápidos, o en entornos de alta vibración (como vehículos), añada un margen adicional 10-30%.
• Efectos de la temperatura y la fricción: Para entornos extremos, consultar los datos del fabricante sobre cómo afecta la temperatura al par nominal de la bisagra.
• Corrección del mecanismo de apoyo: Si el sistema tiene asistencias (por ejemplo, resortes de gas, resortes de torsión), el par de asistencia puede restarse del par total. $T_{texto{de{agarre}} = T_{texto{máx}} - $.

Verificación y depuración de diseños

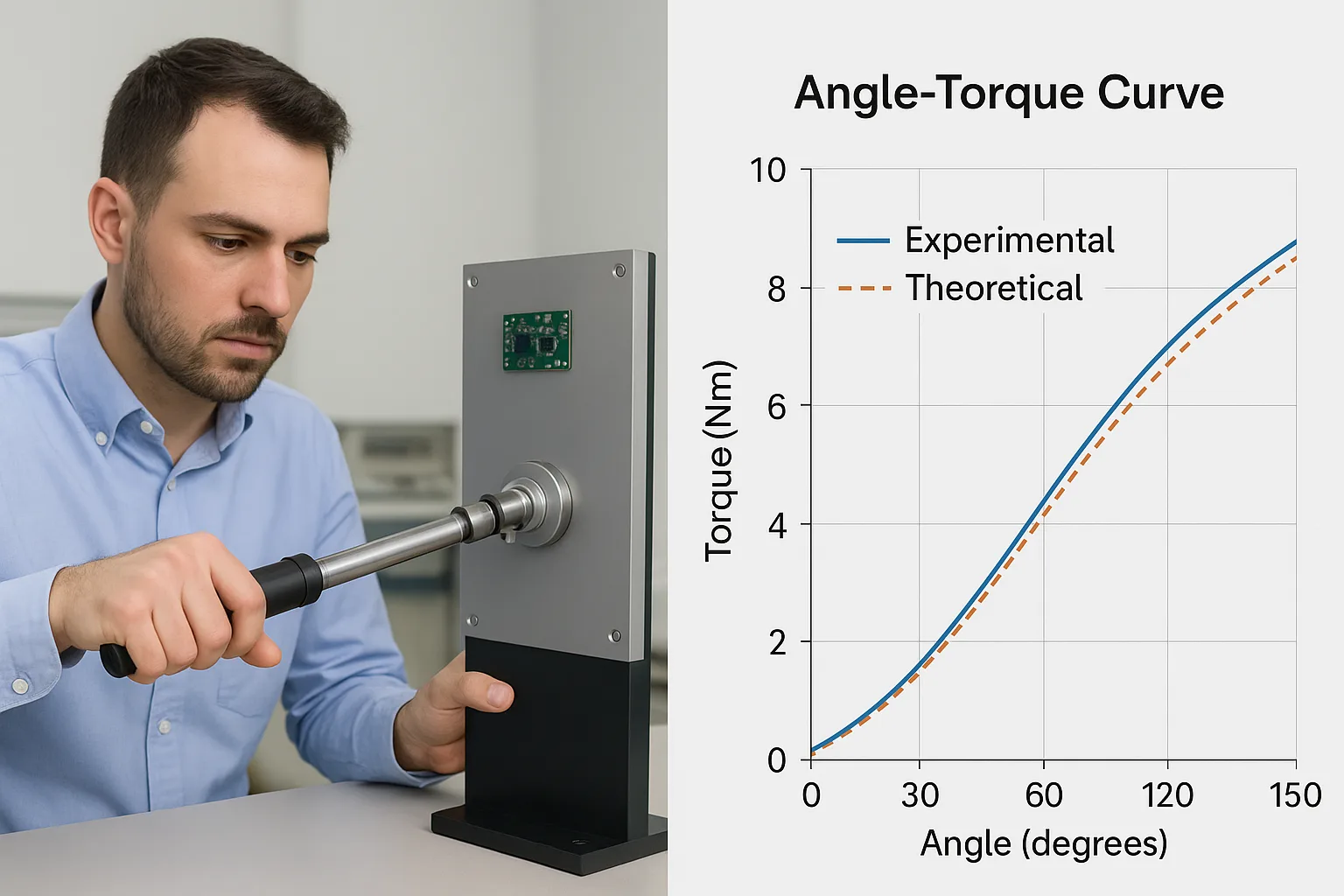
Prueba de rendimiento de la bisagra de torsión y curva ángulo-torsión

• Validación experimental: Utilice una llave dinamométrica en un prototipo para medir la fuerza real de apertura/cierre en múltiples ángulos, especialmente si se requiere un posicionamiento de parada libre. Compare los resultados empíricos con los valores calculados para garantizar la precisión del diseño.
• Simulación de software: Utilice software CAD y de análisis de movimiento para simular el ciclo de apertura y visualizar la curva ángulo-par.
• Depuración y optimización: Si la resistencia a la apertura es demasiado alta, considere reducir la fricción de la bisagra o reposicionar el centro de gravedad. Si el panel se hunde, debe aumentar el par nominal de la bisagra.

Pautas de diseño del par para distintas aplicaciones

• Cubiertas para equipos industriales: Prioriza el par elevado y la durabilidad para un uso frecuente y un enclavamiento seguro.
• Pantallas de dispositivos médicos: Enfatiza el posicionamiento suave y preciso y una sensación consistente. A menudo utiliza bisagras de torsión de precisión con tolerancias estrictas (por ejemplo, ±20%).
• Puertas de vehículos y paneles de acceso: Deben tener en cuenta vibraciones e impactos elevados, lo que a menudo exige el cumplimiento de normas específicas de automoción(SAE J934_2019).
• Carcasas electrónicas (por ejemplo, bisagras para portátiles): Requiere una larga vida útil, miniaturización y un par extremadamente constante en un tamaño reducido.

Principios clave de diseño y resumen

• Parámetros básicos: El diseño se rige por el peso del panel ($W$), la distancia del centro de gravedad ($d$) y el número de bisagras ($N$).
• Fórmula y modificaciones: Calcular el par estático máximo utilizando $T_{text{max}} = Wgd$ (para la posición horizontal). Aplique un factor de seguridad (1,2-1,5) y cualquier corrección dinámica/ambiental.
• Verificación: Valide siempre sus cálculos con un prototipo físico o una simulación precisa.
• Posicionamiento de parada libre: Si el diseño requiere mantener una posición en cualquier ángulo, especifique bisagras de torsión (bisagras de fricción). Proporcionan una resistencia constante para permitir la función "tocar para parar".

Mediante el cálculo y la validación sistemáticos, los ingenieros pueden garantizar que el par de las bisagras cumple la funcionalidad del producto e incorpora los márgenes de seguridad necesarios.

Anexo

A. Tabla de conversión de unidades de par

Unidad	Conversión
N-m	1 N-m = 10,197 kgf-cm = 8,851 lbf-in
kgf-cm	1 kgf-cm = 0,09807 N-m
lbf-in	1 lbf-in = 0,11298 N-m

B. Rangos de par de referencia para bisagras comunes

Escenario de aplicación	Rango de par común (total)
Pequeños dispositivos electrónicos	0,1-2 N-m
Pantallas médicas/de instrumentos	1-5 N-m
Armarios industriales	5-20 N-m
Escotillas para maquinaria pesada	20-50 N-m (y superior)