Berechnung des Scharnierdrehmoments: Eine Schritt-für-Schritt-Anleitung

Das Scharnierdrehmoment ist ein entscheidender Parameter bei der Konstruktion von Drehabdeckungen, Türverkleidungen oder Displays. Es bestimmt den Dämpfungseffekt und das Gleichgewicht beim Öffnen und Schließen der Komponenten. Eine falsche Auslegung des Drehmoments kann dazu führen, dass Paneele unkontrolliert herunterfallen, das Öffnen erschwert wird oder es zu Sicherheitsvorfällen kommt. Das Verständnis der Drehmomentberechnung ist für die Verbesserung der Produktsicherheit und der Benutzerfreundlichkeit unerlässlich.

Dieser Artikel beginnt mit der physikalischen Definition des Drehmoments, analysiert systematisch die Einflussfaktoren und Berechnungsformeln und veranschaulicht den Prozess anhand praktischer Beispiele. Dieser Artikel behandelt die Definition des Drehmoments, Schlüsselvariablen, Berechnungsbeispiele, Sicherheitsfaktoren und Überprüfungsmethoden und ermöglicht es den Konstrukteuren, die wesentlichen Prinzipien schnell zu erfassen.

Kernfunktionen des Scharnierdrehmoments

Unterstützung und Dämpfung

Die Scharniere tragen das Gewicht des Paneels und bieten Widerstand beim Öffnen, so dass die Stabilität in jedem Winkel gewährleistet ist.

Gleichgewicht und Sicherheit

Ein angemessenes Drehmoment ermöglicht ein ausgewogenes Öffnen der Platte und verhindert, dass sie plötzlich unter ihrem eigenen Gewicht herunterfällt. Ein unzureichendes Drehmoment führt zu einer Absturzgefahr, während ein übermäßiges Drehmoment das Öffnen erschwert und eine Spannungskonzentration verursachen kann.

Verbesserte Bedienbarkeit

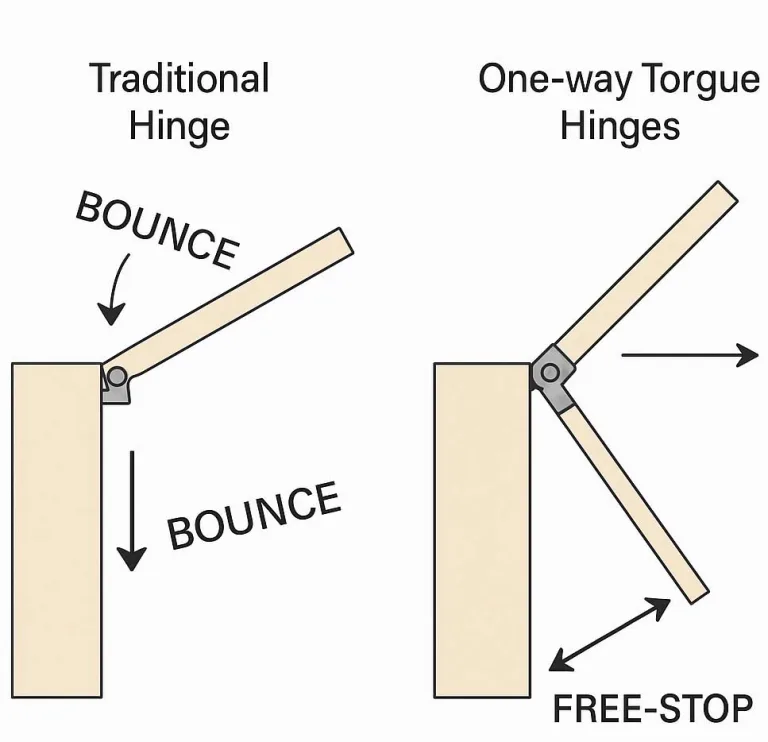
Drehmomentscharniere (oder "Friktionsscharniere") ermöglichen die Positionierung des freien Anschlags in jedem beliebigen Winkel ohne zusätzliche Stützmechanismen.

Zielsetzung

In diesem Artikel werden schrittweise die Definition, die Berechnungsformel und der Konstruktionsprozess für das Scharnierdrehmoment erläutert. Er umfasst: die Definition der Berechnungsformel, die Bereitstellung von Schritt-für-Schritt-Beispielen, die Einführung von Sicherheitsfaktor-Anpassungen und die Beschreibung von Überprüfungsmethoden. Abschließend werden Hinweise zur Auswahl des Drehmoments für verschiedene Anwendungsszenarien gegeben, damit Ingenieure die Auslegung von Scharnierdrehmomenten meistern können.

Die Grundlagen verstehen: Was ist ein Scharnierdrehmoment?

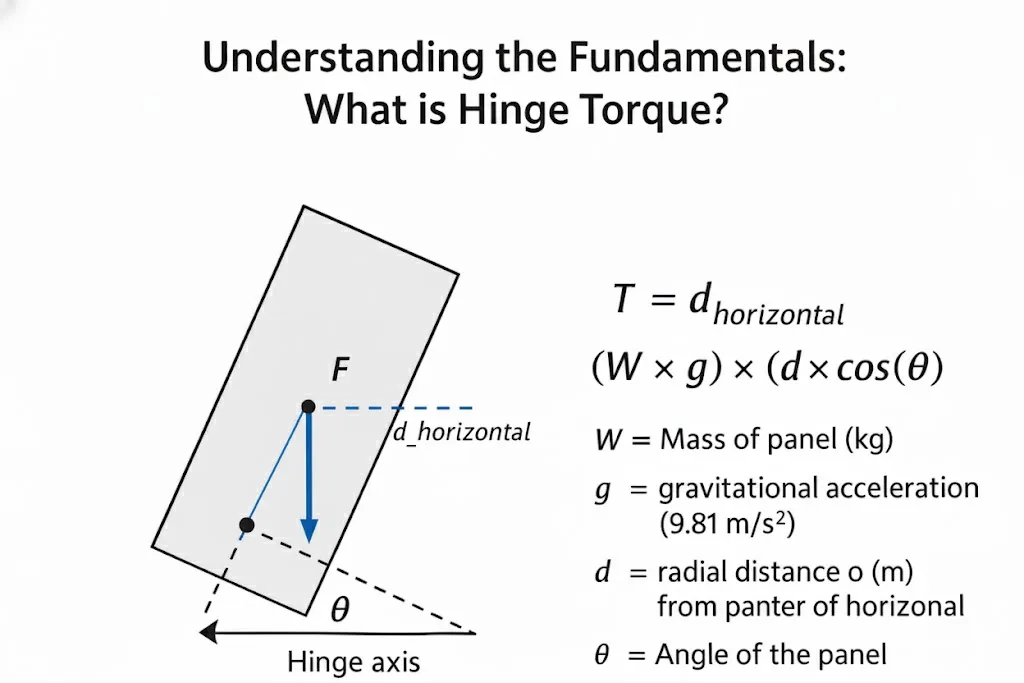
Definition und Berechnung des Scharniermoments

Physikalische Definition

Das Drehmoment ($T$) ist die Rotationskraft, definiert als die aufgebrachte Kraft ($F$) multipliziert mit der Hebelarmlänge ($d$). Bei einem Scharnier ist die primäre Kraft das Gewicht der Platte (Masse $\mal$ Schwerkraftbeschleunigung), das auf den Schwerpunkt der Platte wirkt. Das Drehmoment wird üblicherweise in N-m (Newton-Meter) gemessen.

Die grundlegende Formel lautet wie folgt:
$T = F \times d_{\text{horizontal}} = (W \times g) \times (d \times \cos(\theta))$

Wo:

• $W$ = Masse der Platte (kg)
• $g$ = Gravitationsbeschleunigung (≈9,81 m/s²)
• $d$ = der radiale Abstand (geradliniger Abstand) vom Plattenschwerpunkt zur Scharnierachse (m)
• $d_{\text{horizontal}}$ = Der horizontale Hebelarm (m), der die Komponente von $d$ ist, die tatsächlich ein Drehmoment erzeugt. Er wird berechnet als $d_{\text{horizontal}} = d \mal \cos(\theta)$
• $\theta$ = Der Winkel der Platte gegenüber der horizontalen Ebene.
• Die grundlegende Formel lautet wie folgt:

T=F×dhorizontal=(W×g)×(d×cos(θ))T = F \times d_{\text{horizontal}} = (W \times g) \times (d \times \cos(\theta))T=F×dhorizontal=(W×g)×(d×cos(θ))

Diese Formel zeigt korrekt, dass das Drehmoment MAXIMAL ist ($T = Wgd$), wenn die Platte horizontal ist ($\theta = 0°$), da der Hebelarm am längsten ist. Das Drehmoment wird NULL, wenn die Platte vertikal ist ($\theta = 90°$), da die Wirkungslinie des Plattengewichts durch die Scharnierachse verläuft und der Hebelarm praktisch Null ist.

Statisches Drehmoment vs. dynamisches Drehmoment

• Statisches Drehmoment: Die Rotationskraft, die erforderlich ist, um die Platte in einem bestimmten Winkel zu halten (Überwindung der Schwerkraft). Dies ist der Hauptschwerpunkt unserer Berechnung.
• Dynamisches Drehmoment: Das zusätzliche Drehmoment, das zur Überwindung der Trägheit (zum Starten oder Anhalten der Bewegung) und der Dämpfungskräfte erforderlich ist.

Die Konstruktion konzentriert sich in der Regel zunächst auf die Berechnung des maximalen statischen Drehmoments und berücksichtigt dann die dynamischen Effekte je nach Anwendung.

Funktionale Rolle im Design

Das Drehmoment der Scharniere steuert das Gleichgewicht der Platte, ermöglicht die Positionierung des freien Anschlags und verhindert ein plötzliches Schließen. Drehmomentscharniere verwenden beispielsweise interne Reibungsmechanismen, um Abdeckungen zu fixieren. Ein angemessenes Drehmoment gewährleistet einen stabilen, reibungslosen Betrieb.

Schlüsselfaktoren, die das Scharnierdrehmoment beeinflussen

Abdeckung Gewicht (W): Das Drehmoment ist direkt proportional zum Gewicht der Platte.

Körperschwerpunkt (d): Je größer der horizontale Abstand (Hebelarm) vom Plattenschwerpunkt zur Scharnierachse ist, desto höher ist das erforderliche Drehmoment. Bei asymmetrischen Platten muss der tatsächliche Schwerpunkt ermittelt werden.

Anzahl der Scharniere (N): Mehrere Scharniere teilen sich die gesamte Drehmomentbelastung. Bei einer symmetrischen Anordnung ist das Gesamtdrehmoment im Idealfall gleichmäßig verteilt: $T_{\text{pro_Scharnier}} = T_{\text{max}} / N$ (Geht von einer symmetrischen Lastverteilung aus. Bei asymmetrischen Platten, bei denen der Schwerpunkt nicht mittig zwischen den Scharnieren liegt, ist das Gesamtdrehmoment ($T_{\text{max}}$) immer noch das Ziel. Die Konstrukteure müssen jedoch sicherstellen, dass die Platte ausreichend steif ist, um ein Verziehen oder Verdrehen während des Betriebs zu verhindern).

Installationswinkel und Rotationsbereich ($\theta$): Das Drehmoment ist maximal, wenn die Platte horizontal ($\theta = 0°$) und minimal (Null), wenn sie vertikal ($\theta = 90°$) ist. Bei den Konstruktionsberechnungen muss immer das Szenario des maximalen Drehmoments (die horizontale Position) zugrunde gelegt werden.

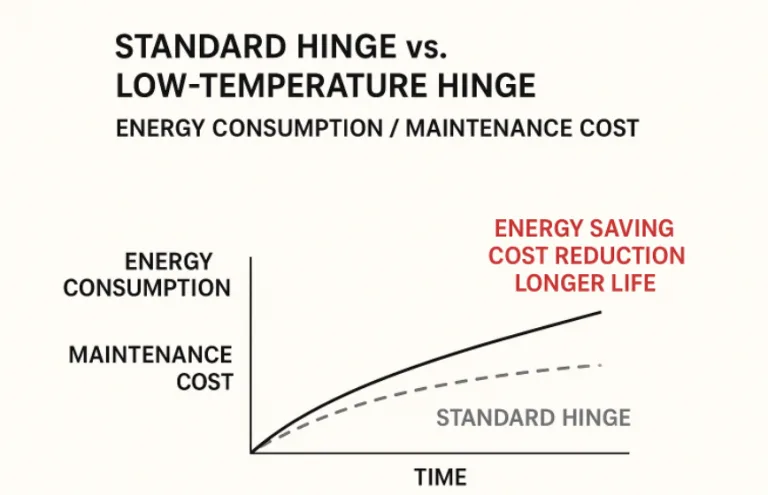
Dämpfung und Reibung: Die innere Reibung in Drehmomentscharnieren sorgt für die "Haltekraft". Umgebungsfaktoren wie Temperatur, Staub oder Schmierungsbedingungen können das tatsächliche Drehmoment beeinflussen. Hohe Temperaturen können die Viskosität des Dämpfungsfetts verringern (wodurch das Drehmoment sinkt), während niedrige Temperaturen oder Verschmutzung die Reibung erhöhen können(Laesecke et al. (2019), NIST).

Formelberechnung und Schrittanalyse

Grundlegende Formel

Die grundlegende Berechnung des Scharnierdrehmoments lautet:
$T = W \Mal g \Mal d \Mal \cos(\Theta)$

Für Konstruktionszwecke muss das maximale Drehmoment ($T_{\text{max}}$) ermittelt werden, das auftritt, wenn die Platte waagerecht ist ($\theta = 0°$, d. h. $\cos(0°) = 1$).

Die Formel lautet vereinfacht:
$T_{\text{max}} = W \Zeiten g \Zeiten d$

Die Bezugsformel eines Scharnierlieferanten, wie z. B. "Drehmoment $T = L/2 \mal m \mal 9,8$ (in N-m)", basiert auf genau diesem Prinzip. Sie geht davon aus:

• $m$ = Masse ($W$)
• $L/2$ = Schwerpunktsabstand ($d$), unter der Annahme einer gleichmäßigen Platte, bei der der Schwerpunkt bei der Hälfte der Länge/Breite liegt.

Beispiel: Für eine Platte mit $L=0,3$ m (also $d=0,15$ m) und $m=2$ kg beträgt das maximale Drehmoment:
$T_{\text{max}} = 0,15 \text{ m} \times 2 \text{ kg} \mal 9,81 \text{ m/s}^2 \ca. 2,94$ N-m.

Berechnungsschritte

Schritt eins: Berechnen des gesamten maximalen Drehmoments ($T_{\text{max}}$)

Verwenden Sie immer die Formel für die horizontale Position ($T_{\text{max}} = Wgd$), um die ungünstigste Belastung zu ermitteln.

Beispiel: Eine Platte hat eine Masse ($W$) von 8 kg, und ihr Schwerpunkt ($d$) liegt 0,25 m von der Gelenkachse entfernt.
$T_{\text{max}} = W \Zeiten g \Zeiten d$
$T_{\text{max}} = 8 \text{ kg} \mal 9,81 \text{ m/s}^2 \mal 0,25 \text{ m} \cax$ 19,62 N-m

Diese 19,62 N-m sind das gesamte statische Drehmoment, das das Scharniersystem aufnehmen können muss, um die Platte in ihrer schwersten Position (horizontal) zu halten.

Schritt zwei: Verteilung des Scharnierdrehmoments

Berechnungsschritte: Gelenkmomentverteilung (symmetrische Belastung)

Wenn Sie mehrere Scharniere verwenden, teilen Sie das maximale Gesamtdrehmoment durch die Anzahl der Scharniere ($N$).

Im obigen Beispiel sind es bei Verwendung von $N=2$ Scharnieren:
$T_{\text{pro_Scharnier}} = T_{\text{max}} / N = 19,62 / 2 \cax$ 9,81 N-m pro Scharnier.

Sie würden dann zwei Scharniere auswählen, die nach Anwendung von Sicherheitsfaktoren für mindestens 9,81 N-m ausgelegt sind.

Berücksichtigung von Korrektur- und Sicherheitsfaktoren

• Sicherheitsfaktor: Sicherheitsfaktor: Multiplizieren Sie $T_{\text{max}}$ mit 1.2-1.5 um Montagefehler, Materialalterung und Fertigungstoleranzen zu berücksichtigen. Für schnelle Bewegungen oder Umgebungen mit starken Vibrationen ist eine zusätzliche Marge von 10-30% zu berücksichtigen. Bei extremen Temperaturen konsultieren Sie die Herstellerangaben für Drehmomentschwankungen aufgrund von Viskositätsänderungen des Dämpfungsfetts.
• Dynamische Lastkorrektur: Für schnelles Öffnen/Schließen oder in Umgebungen mit starken Vibrationen (z. B. in Fahrzeugen) ist eine zusätzliche Marge von 10-30% erforderlich.
• Temperatur- und Reibungseffekte: Bei extremen Umgebungsbedingungen konsultieren Sie die Herstellerangaben zu den Auswirkungen der Temperatur auf die Drehmomentwerte des Scharniers.
• Korrektur der Stützmechanismen: Verfügt das System über Hilfskräfte (z. B. Gasfedern, Torsionsfedern), kann das Hilfsdrehmoment vom Gesamtdrehmoment abgezogen werden. $T_{\text{Gelenk}} = T_{\text{max}} - T_{\text{Assist}}$.

Entwurfsverifizierung und Fehlersuche

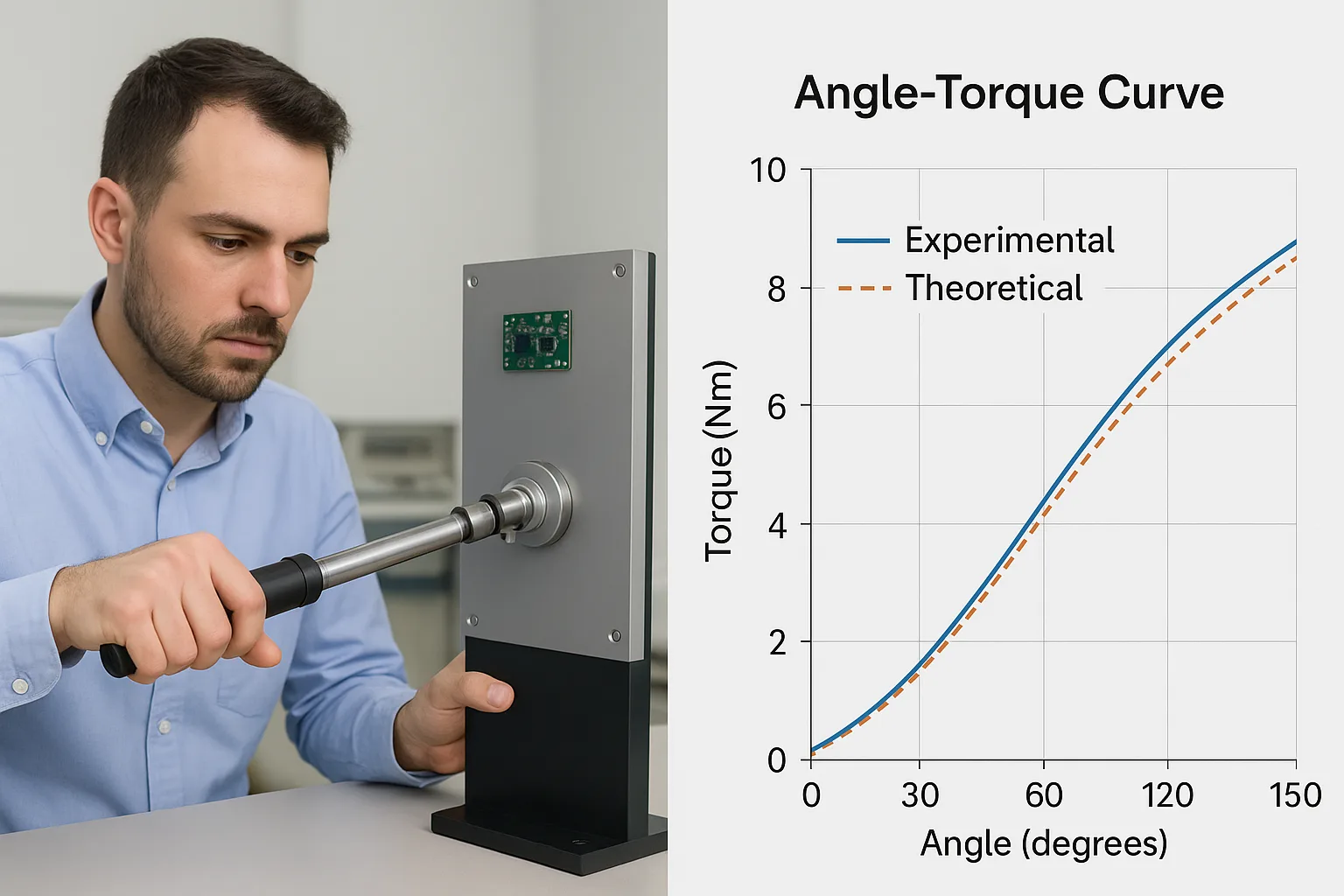
Drehmoment-Scharnierleistungstest und Winkel-Drehmoment-Kurve

• Experimentelle Validierung: Verwenden Sie einen Drehmomentschlüssel an einem Prototyp, um die tatsächliche Öffnungs-/Schließkraft in verschiedenen Winkeln zu messen, insbesondere wenn eine Positionierung ohne Anschlag erforderlich ist. Vergleichen Sie die empirischen Ergebnisse mit den berechneten Werten, um die Genauigkeit der Konstruktion sicherzustellen.
• Software-Simulation: Verwenden Sie CAD- und Bewegungsanalyse-Software, um den Öffnungszyklus zu simulieren und die Winkel-Drehmoment-Kurve zu visualisieren.
• Fehlersuche und Optimierung: Wenn der Öffnungswiderstand zu hoch ist, sollte die Reibung der Scharniere verringert oder der Schwerpunkt verlagert werden. Wenn die Platte durchhängt, müssen Sie das Drehmoment der Scharniere erhöhen.

Richtlinien für die Drehmomentgestaltung für verschiedene Anwendungen

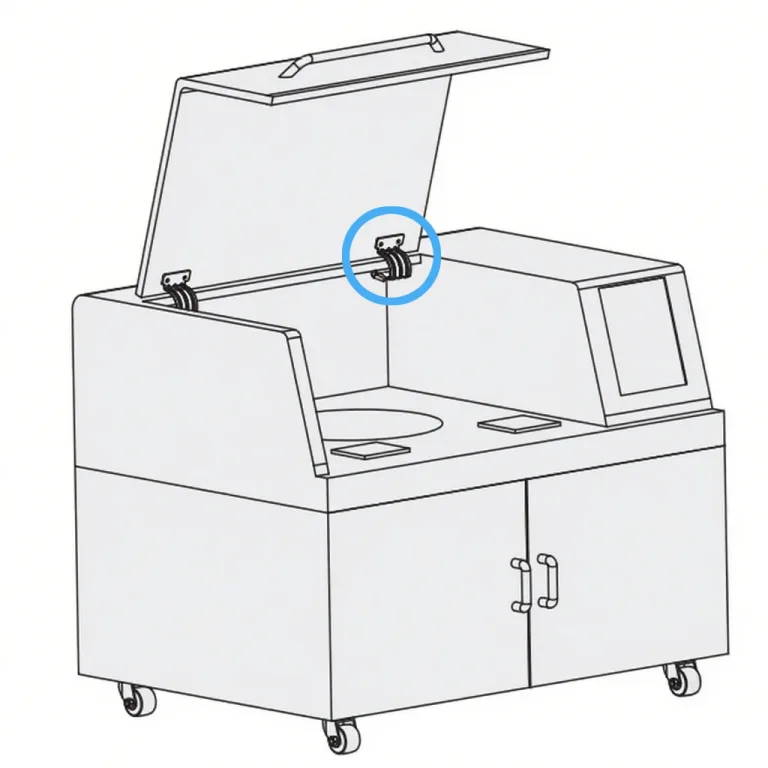
• Abdeckungen für Industrieanlagen: Hohe Drehmomente und Langlebigkeit für häufigen Gebrauch und sicheres Einrasten stehen im Vordergrund.
• Displays für medizinische Geräte: Legt Wert auf eine sanfte, präzise Positionierung und ein einheitliches Gefühl. Verwendet oft Präzisions-Drehmomentscharniere mit engen Toleranzen (z. B. ±20%).
• Fahrzeugtüren und Zugangspaneele: Müssen hohen Vibrationen und Stößen standhalten, was oft die Einhaltung spezifischer Automobilstandards erfordert(SAE J934_2019).
• Elektronikgehäuse (z. B. Laptop-Scharniere): Hohe Lebensdauer, Miniaturisierung und ein extrem gleichmäßiges Drehmoment in einem kleinen Gehäuse sind erforderlich.

Zentrale Gestaltungsprinzipien und Zusammenfassung

• Kernparameter: Das Design wird durch das Gewicht der Platte ($W$), den Schwerpunktabstand ($d$) und die Anzahl der Scharniere ($N$) bestimmt.
• Formel und Modifikationen: Berechnen Sie das maximale statische Drehmoment mit $T_{\text{max}} = Wgd$ (für die horizontale Position). Wenden Sie einen Sicherheitsfaktor (1,2-1,5) und eventuelle dynamische/umweltbedingte Korrekturen an.
• Überprüfung: Überprüfen Sie Ihre Berechnungen immer anhand eines physischen Prototyps oder einer genauen Simulation.
• Frei-Stopp-Positionierung: Wenn die Konstruktion das Halten einer Position in einem beliebigen Winkel erfordert, sind Drehmomentscharniere (Reibungsscharniere) zu verwenden. Diese bieten einen konstanten Widerstand, um die "Touch-to-Stop"-Funktionalität zu ermöglichen.

Durch systematische Berechnung und Validierung können Ingenieure sicherstellen, dass das Drehmoment der Scharniere sowohl die Produktfunktionalität erfüllt als auch die erforderlichen Sicherheitsmargen berücksichtigt.

Anhang

A. Umrechnungstabelle für Drehmomenteinheiten

Einheit	Konvertierung
N-m	1 N-m = 10,197 kgf-cm = 8,851 lbf-in
kgf-cm	1 kgf-cm = 0,09807 N-m
lbf-in	1 lbf-in = 0,11298 N-m

B. Referenzdrehmomentbereiche für gängige Scharniere

Anwendungsszenario	Gemeinsamer Drehmomentbereich (Gesamt)
Kleine elektronische Geräte	0,1-2 N-m
Medizinische/Instrumentenanzeigen	1-5 N-m
Industrielle Schränke	5-20 N-m
Hochleistungsklappen für Maschinen	20-50 N-m (und mehr)