Torque Hinge Calculation & Selection Guide: Formulas & Standards

Torque hinges (also known as friction hinges or free-stop hinges) introduce controllable damping and holding torque within a rotational joint. They allow a cover, display, or door to hold its position at any angle without spring-back, ensuring a consistent feel during opening and closing.

In laptops, industrial equipment service doors, medical display arms, and precision instruments, these hinges directly affect HMI (Human-Machine Interface) quality, product lifetime, and safety.

This comprehensive guide provides practical torque calculation methods, a selection workflow, material essentials, and technical standard references to streamline your design process.

Basic Principles of Torque Hinges

Definition and Physical Meaning

Torque ($T$): The rotational force, defined as the product of the applied force and the moment arm.

• Unit: N·m (Newton-meter), per ISO 80000-4:2019 quantities and units in mechanics.

In a hinge structure, gravity generates a gravitational moment via the perpendicular distance from the panel’s center of gravity to the rotation axis. The hinge’s internal friction pair produces a resisting friction torque. The balance between the two determines whether the part holds its position.

Static Torque vs. Dynamic Torque

When selecting a hinge, it is critical to distinguish between these two concepts:

• Static Torque: The torque required to hold the panel stationary at a specific angle against gravity. Design calculations primarily focus on this value.
• Dynamic Torque: The torque required to move the panel (overcoming inertia and kinetic friction).
  • Note: High-viscosity damping grease typically causes dynamic torque to be slightly higher than static torque. This prevents “bouncing” but requires slightly more force from the user to initiate movement.

Working Mechanism

Internally, stacked friction plates (e.g., steel/phosphor bronze) or preloaded elastic elements create constant or near-constant damping.

• Holding Condition: When Friction Torque ≥ External Disturbance Torque (Gravity + Vibration), the angle is stably “locked.”
• Relevant Tests:
  • ISO 4287/4288: Surface roughness parameters and assessment.
  • ASTM G99: Pin-on-disk wear test to evaluate friction pair longevity.

Classification by Structural Form

Key Parameters for Torque Hinge Selection

Basic Quantities Needed

• Weight ($W$): In Newtons (N). Formula: $W = Mass (kg) \times 9.81 m/s²$.
• Moment Arm ($L$): The perpendicular distance from the Center of Gravity (COG) to the rotation axis (meters).
• Angle ($\theta$): The angle relative to the direction of gravity.
• Hinge Count ($n$): Determines the torque share per hinge.

The Torque Calculation Formula

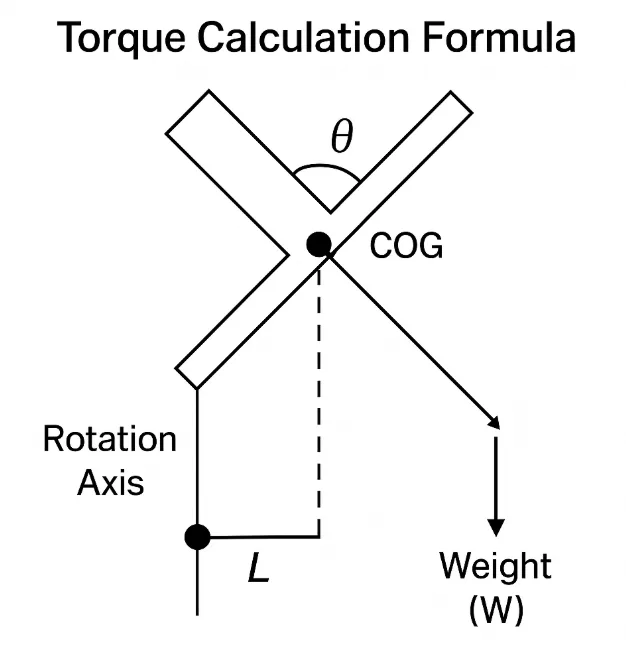
The fundamental requirement for a holding position is:

$$T_{req} = W \times L \times \sin(\theta)$$

Note: $\theta$ represents the angle where gravity has the maximum leverage. This peak almost always occurs when the panel is horizontal ($\sin 90^\circ = 1$).

Design Formula (with Safety Factor):

$$T_{design} = SF \times T_{req}$$

• Recommended Safety Factor (SF): 1.2 – 1.5 (Accounts for manufacturing tolerances, grease viscosity changes, and wear).
• T_design defines your target selection range.

Common Pitfalls

Warning:

• Mass vs. Weight: Do not use Kg directly. You must convert to Newtons ($kg \times 9.81$).
• Geometric Center vs. COG: Do not assume the geometric center is the Center of Gravity (COG). For asymmetrical panels, find the true COG in CAD.
• The Horizontal Trap: The peak torque requirement is determined when the lever arm is longest (horizontal). Always calculate for this worst-case scenario.

Calculation Examples by Application

Laptop Display (Lightweight/Precision)

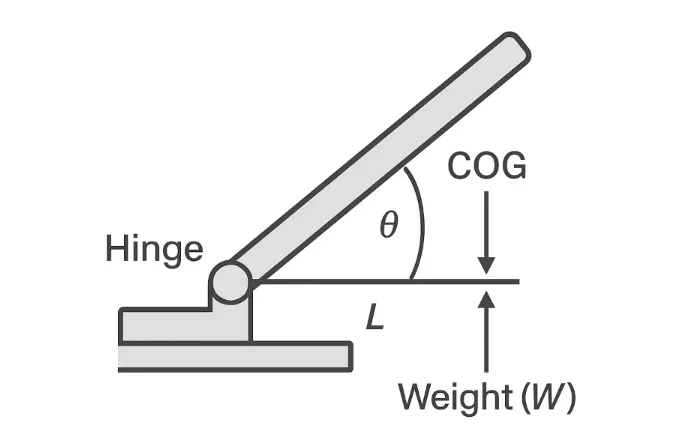
• Conditions: Display mass 0.45 kg ($W \approx 4.415 N$); COG distance $L = 0.10 m$.
• Peak Condition: Horizontal (open 90° or 180° depending on layout).
• Calculation:$$T_{req} = 4.415 N \times 0.10 m = 0.4415 N\cdot m$$
• Design Target (SF = 1.3):$$T_{design} = 0.4415 \times 1.3 = 0.574 N\cdot m$$
• Selection: Two hinges sharing the load $\rightarrow$ ~0.29 N·m per hinge.

Industrial Service Cover (Heavy Duty)

• Conditions: Steel cover mass 3.0 kg ($W = 29.43 N$); COG distance $L = 0.18 m$.
• Calculation:$$T_{req} = 29.43 N \times 0.18 m = 5.30 N\cdot m$$
• Design Target (SF = 1.3):$$T_{design} = 5.30 \times 1.3 = \mathbf{6.89 N\cdot m}$$
• Selection: Two hinges $\rightarrow$ ~3.45 N·m per hinge.
• Note: For vibrating environments (generators, compressors), increase SF to 1.5 or 2.0 to prevent “creep.”

Medical Display Arm (Multi-Joint)

• Approach: Model each joint independently.
  • Joint A (Base): Carries the full arm + display weight.
  • Joint B (End): Carries only the display.
• Requirement: Medical environments often require specific material compatibility (cleaners) and particle emission controls (ISO Class cleanrooms).For a complete step-by-step calculation with real values, see How to Calculate Torque Hinge Requirements: Industry Case Studies.

Materials and Environmental Durability

Corrosion Note: For outdoor or chemical settings, prioritize 316L stainless steel or hard anodic coatings. Verify performance via cyclic damp heat tests (IEC 60068-2-30).

Selection Workflow (Checklist)

1. Define Orientation: Determine rotation range and the “Peak Angle” (where gravity acts strongest).
2. Calculate Peak Torque: $T_{req} = W \times L_{COG}$.
3. Apply Safety Factor: Multiply by 1.2–1.5 to get $T_{design}$.
4. Determine Load Sharing: Divide by the number of hinges ($n$).
5. 5. Select Model: Match torque range and curve type (Uni/Bi-directional).
6. Prototype Verification: Test for “feel,” backlash, and temperature drift (-20°C to +60°C).

Installation and Alignment Guide

Correct installation is just as critical as correct selection. Even a well-specified torque hinge will underperform or wear prematurely if mounting surfaces are misaligned or fasteners are over-torqued.

Mounting Surface Requirements

• Flatness and rigidity: Mounting surfaces must be flat and sufficiently stiff. Even a 0.5° misalignment between two hinge axes creates a binding condition that accelerates friction-pair wear and causes inconsistent torque output.
• Multi-hinge co-linearity: When installing two or more hinges on the same panel, all pivot axes must be co-linear. Temporarily clamp the panel in position and verify alignment before committing to final fastener torque.
• Surface finish: Avoid painted or powder-coated surfaces where coating buildup can introduce a gap under the hinge leaf, causing rocking and uneven load transfer. Bare metal contact is preferred for precision applications.

Fastener Selection and Torque Control

• Match fastener material to hinge material to prevent galvanic corrosion — use 316 SS screws with 316 SS hinges, zinc-plated screws with carbon steel hinges.
• Use a torque-limiting driver for small hinges. Over-tightening is one of the most common installation errors: excessive clamping force deforms the hinge housing and permanently shifts the torque value. Small hinges typically require only 0.6 – 1.1 N·m (5 – 10 in·lbf) of fastener torque.
• Apply thread-locking compound (e.g., medium-strength Loctite 243) in high-vibration environments such as generators, compressors, or transportation equipment to prevent gradual loosening.

Adjustable Hinge Field Setup

For adjustable torque hinges, do not pre-set the target resistance before installation. The correct sequence is:

1. Install the hinge at the lowest torque setting.
2. Mount the panel and verify free movement through the full rotation range.
3. Increase the adjustment screw in small increments while testing panel hold at the critical angle (usually horizontal).
4. Stop when the panel holds position without drooping and opens smoothly with acceptable user effort.
5. Record the final adjustment setting (screw turns from minimum, or measured torque value) for maintenance reference.

Installation Tip: For critical applications, perform a post-installation verification by measuring actual hinge torque output with a torque gauge at 30°, 60°, and 90° to confirm consistency within the ±10% specification window.

Maintenance and Service Life

Torque hinge service life depends on load, cycle frequency, environment, and maintenance quality. Understanding the right maintenance approach for each hinge type prevents unexpected failures and avoids unnecessary replacements.

Sealed vs. Unsealed Maintenance Requirements

Routine Inspection Checklist

• Visual: Check for surface corrosion, cracks at mounting holes, deformed hinge leaves, or discoloration indicating heat exposure.
• Mechanical feel: Manually cycle through the full rotation range. Resistance should feel consistent. Sudden light spots, heavy spots, or grinding indicates internal wear or debris ingress.
• Fastener check: Verify all mounting screws remain at specified torque. Loose fasteners shift the hinge axis and accelerate side-loading wear.
• Torque measurement (high-cycle applications): Use a torque gauge to measure actual holding force at 90°. If the measured value drops below 80% of the original specification, schedule replacement before failure occurs.

Lubricant Selection by Environment

Note: Adding standard grease to a sealed hinge designed for dry-film friction elements will reduce torque consistency and shorten service life. Always confirm the lubrication type with the manufacturer before field servicing.

Troubleshooting Guide

The table below consolidates symptom-based diagnosis with root-cause analysis and validated remediation strategies. For temperature-related failures, verify corrective actions against IEC 60068-2-14 (Thermal shock test).

Torque Unit Conversion Table

Typical Torque Reference Ranges

• Small Electronics (Phones/Tablets): 0.1 – 0.6 N·m
• Laptops: 0.4 – 0.8 N·m (per hinge)
• Medical/POS Displays: 1.5 – 5.0 N·m
• Industrial Cabinets: 5.0 – 15.0 N·m
• Heavy Machinery Hatches: 20.0+ N·m (Usually requires Counterbalance Hinges or Gas Struts)

FAQ

Q1: Should I use mass or weight for selection?

Always use Weight (N). If you have mass ($kg$), calculate $W = kg \times 9.81$.

Q2: Why does the peak torque usually occur at horizontal?

Because at 90° (horizontal), the lever arm of gravity relative to the hinge axis is at its maximum length, creating the highest gravitational moment.

Q3: Do two hinges share the load perfectly equally?

Not perfectly. Assembly bias and friction differences lead to unequal sharing. This is why we apply a Safety Factor of at least 20%.

Q4: How to balance “light feel” and “strong holding”?

Use an angle-dependent torque curve (where torque is higher only at holding angles) or a composite scheme (friction hinge + gas strut) to provide lift assistance.

Q5: What is the typical service life of a torque hinge?

Standard-grade torque hinges are rated for 10,000 – 25,000 cycles under specified load and temperature conditions. Premium industrial or medical-grade models using hardened shafts and PEEK friction elements typically achieve 50,000+ cycles. Service life shortens significantly when operating above rated load, in temperatures outside the specified range, or without adequate maintenance. For high-cycle applications (daily operation, production line equipment), specify hinges with documented cycle life test reports per ASTM F1574.

Q6: Can a torque hinge be repaired or recalibrated after torque decay?

Sealed torque hinges with factory-set friction elements are generally not field-serviceable — when torque drops below 80% of specification, replacement is the correct action. Adjustable torque hinges can be recalibrated on-site by tightening the adjustment screw to compensate for minor wear. For large industrial hinges with replaceable friction discs, factory-authorized rebuilding is possible but only cost-effective when the hinge cost significantly exceeds replacement price.

Q7: How does temperature affect torque output?

Temperature is one of the most significant environmental variables. As a general rule: torque increases in cold (grease stiffens, friction rises) and decreases in heat (grease thins, friction drops). Standard hinges with petroleum-based grease typically show ±20% torque drift across the −10°C to +70°C range. For applications requiring tight torque consistency across a wide temperature range — medical equipment, outdoor enclosures, automotive interiors — specify hinges with low-drift friction pairs and validate performance against IEC 60068-2-14 thermal shock testing.

Q8: Are torque hinges suitable for outdoor or high-humidity environments?

Yes, with correct specification. Key requirements for outdoor use: (1) housing material should be 316L stainless steel for salt-spray resistance exceeding 500 hours per ISO 9227; (2) sealing should meet at minimum IP54 to prevent dust and water ingress; (3) internal lubricant must be rated for the local temperature range. Standard zinc-alloy or carbon steel hinges with basic plating are not suitable for prolonged outdoor exposure and will develop corrosion within months in coastal or industrial-atmosphere environments. See our guide on NEMA 4X hinges for coastal projects for further environmental selection criteria.

Q9: When should I use a single hinge versus two hinges on the same panel?

Single-hinge configurations are acceptable when the panel is narrow, lightweight (under ~1 kg), and the hinge’s rated moment capacity comfortably exceeds the calculated peak torque with a safety factor ≥ 1.5. For panels wider than approximately 200 mm, heavier than 1 kg, or subject to out-of-plane side loading (vibration, operator lateral force), a two-hinge parallel configuration is strongly preferred. Two hinges distribute load evenly, eliminate cantilevered shaft bending, and provide redundancy. Note that real-world load sharing between two hinges is never perfectly equal — always apply a safety factor of at least 1.2 per hinge even in dual configurations. See why torque hinges require matched pairs for the engineering rationale behind pair-matching during procurement.

Q10: What is the difference between a torque hinge and a gas spring for panel support?

Both solve the same functional problem — holding a heavy panel at an angle — but through different mechanisms with different trade-offs:

For panels requiring more than 15 – 20 N·m of support torque, a hybrid approach — torque hinge providing position control combined with a gas strut providing lift assistance — often delivers the best combination of user ergonomics and positional stability. Read more in our comparison guide: Torque Hinges vs Gas Springs vs Springs.